图说文本生成解码策略
之前写过 # Nucleus Sampling与文本生成中的不同解码策略比较,不过文中缺乏图例,对于解码过程解释不够清晰,本文作为2.0版加以补充。
对于文本生成任务,语言模型如何做到对同一个输入生成不同的输出?问题的关键在于解码策略。无论是自编码模型还是自回归模型,都是在解码阶段的每个时间步逐个生成最终文本。所谓解码,就是按照某种策略从候选词表中选择合适的词输出。除了对于模型本身的改进,不同解码策略也对文本生成质量起到重要作用。
不失一般性,语言模型的解码过程可被描述为:给定m个文本序列\(x_1,x_2, \ldots x_m\)作为上下文,生成下n个连续单词从而得到完整的文本序列\(x_1,x_2, \ldots x_m,x_{m+1}, \ldots, x_{m+n}\),生成完整文本序列的概率为:
\[P(x_1,x_2,\ldots,x_{m+n})=\prod_{i=1}^{m+n}{P(x_i|x_1,x_2,\ldots,x_{i-1})}\]
最符合直觉的解码策略显然是最大化文本序列概率的方案。假设词表大小为\(V\),最大文本序列长度为\(L\), 则整个搜索空间是\(V^L\),计算复杂度过高,实践中不可行。容易证明,在词表中找到最可能出现的文本序列是个NP难问题。因此,我们需要用启发式算法来逼近最优解。
贪心搜索
一个直观的简化方案是贪心搜索(Greedy Search),即在每个时间步,都选择最大概率出现的词汇作为下一个词。虽然看上去合理,但它有可能会陷入到不断重复的死循环中。此外,每次选择最高概率单词作为结果的贪心策略,有可能不是全局最优解:即每步都选择了最大概率出现的单词,但生成的句子并不是最合理的。
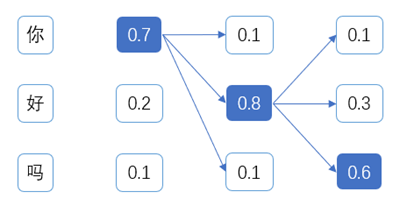
如上图,举例说明贪心搜索的过程:在第一个时间步选择概率最大的单词”你”,在第二个时间步选择概率最大的单词“好”,在给定“你好”的条件下,在第三时间步选择最大概率出现的单词“吗”,最终生成文本”你好吗”,整个句子的生成概率为0.70.80.6=0.336。
集束搜索
前面分析过,如果想找到最优解,需要对整个搜索空间进行遍历,计算量巨大。为解决这个问题,集束搜索(Beam Search)应运而生。它的核心思想是在每个时间步,用上一步K个概率最大的文本序列,与词表中的每个词汇进行组合,并保留前K个生成概率最大的文本序列,为下一步生成做准备。不断重复这个过程,直到遇到终止符或达到最大生成长度为止。相比于贪心搜索,集束搜索通过保留K个文本序列(实践中常用堆进行实现),一定程度上扩大了搜索空间,生成更好的结果。贪心搜索是集束搜索在K=1时的特例。
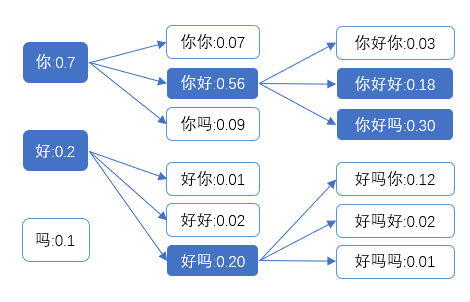
如上图,举例说明K=2时集束搜索的过程:第一个时间步保留两个候选结果“你”和“好”,第二个时间步也保留两个最优结果“你好”和“好吗”,第三个时间步,输出最终结果“你好吗”。
Top-K采样
集束搜索和贪心搜索的思想都是生成最大出现概率的句子。但这样生成的结果可能是短小常见的句子,缺乏信息量。有研究发现:真人说的自然语言常常出人意料,即说出的并不总是语言模型中概率最大的单词。考虑到集束搜索总是选择最大概率出现的单词,因此生成的文本没有新意。
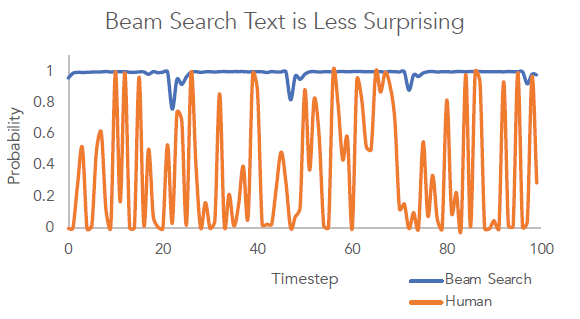
上图很好地说明了集束搜索与真人说话之间的区别,集束搜索生成的句子用词较为常见,但真人的语言所用词汇出现的概率更富有多样性。具体来说,在几个连续时间步里,真人语言所用的词汇很少一直使用高频常见词,而可能会突然转向使用低频但更富有信息量的词汇,这也是真人语言的一个内在属性。当然,这只是后验观察,很难用确定性算法进行精确刻画。不过可以确定,使用集束搜索生成的文本与真人所说文本的概率分布有很大差异,真人语言不是通过最大化句子出现概率的方式产生的。
解决这个问题最直接的方案就是引入采样机制增加随机性,既然集束搜索每次仅关注最好的一个选项,那我们是否可以增加候选词集合的大小,从而达到用词更多样的效果?这就是Top-K采样:在解码的每个时间步取前k个概率最大的词,将它们的概率缩放调整,并按缩放后的概率分布采样得到生成的单词。
本节的Top-K采样和下节介绍的核采样,本质上都是舍弃长尾词并重缩放头部词概率分布的方案。
给定概率分布\(P(x| x_1,x_2,\ldots,x_{i-1})\),定义它的Top-K词表为\(V^{(K)} \subset V\),且\(V^{(K)}\)中的词出现的概率是最大的K个。令\(p'=\sum_{x \in V^{(K)}}P(x|x_1,x_2, \ldots x_{i-1})\),如果\(x \in V^{(K)}\),则将可选词的概率分布重缩放为:
\[P^\prime(x| x_1,x_2,\ldots,x_{i-1})=P^\prime(x| x_1,x_2,\ldots,x_{i-1})/p^\prime\]
否则,令\(P^\prime(x| x_1,x_2,\ldots,x_{i-1})=0\)。
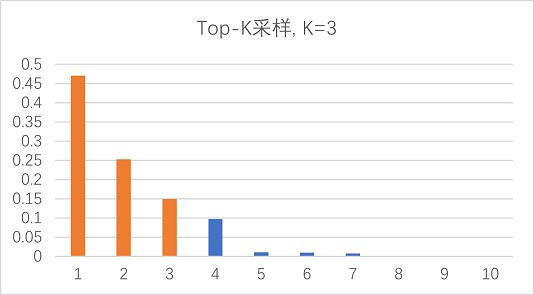
如上图K=3的情况,则在此时间步的可选词将由10个变为概率最高的3个,将它们的概率分布重缩放后进行采样,其他时间步也类似。
核采样(Top-p采样)
但在实践中由于k是个固定值,top-k 采样k的选择是个难题,有时前k个词的概率分布较为均匀,有时概率分布又集中在很少的一些词中,导致有时会生成一些比较通用的词汇,有时会增加采样长尾词的概率,导致语句不通顺。于是,核采样(nucleus sampling,也称Top-p采样)解码策略被提出。它的主要思想是在每个时间步,概率分布总集中在少数关键的“核”词集合,因此我们可以利用概率分布的不同,动态地调整采样集合的大小。即给定一个概率阈值p,从解码词候选集中选择一个最小词表\(V^{(p)}\),使得它们出现的概率和大于等于p:
\[\sum_{x \in V^{(p)}}P(x| x_1,x_2,\ldots,x_{i-1}) \ge p\]
然后与Top-K采样方式一样,针对这个词表对概率分布进行缩放,当前时间步仅从这个词表中解码。这样就实现了在不同时间步,随着解码词的概率分布不同,候选词集合的大小动态变化的效果。由于解码词还是从头部候选集中筛选,这样的动态调整可以使生成的句子在满足多样性的同时又保持通顺。
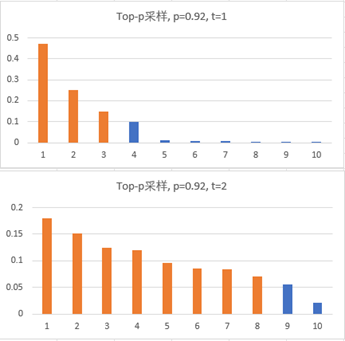
如上图示例,选择p=0.92,第一时间步,候选词集合由10个变为3个;第二时间步,候选词集合由10个变为8个,由于不同时间步之间随候选词概率分布不同,候选词集合的大小也随之动态调整。
温度采样
除了上述几种策略外,温度采样(Temperature Sampling)也是一种常见的解码策略,思路很简单,直接缩放原有的解码词分布,略微修改下softmax函数:
\[p(x=V_l| x_1,x_2,\ldots,x_{i-1})=\frac{exp(u_l/t)}{\sum_{i \in V_l}exp(u_i/t)}\]
其中u是logits,T即温度,是一个超参数,取值范围[0,1),T的取值不同,解码词的概率分布也就更平缓或更两极分化。可以通过设置不同的T达到与top-k和top-p采样类似的效果。
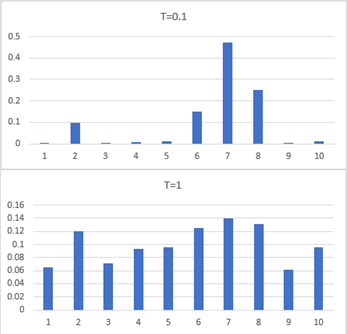
由上图可见,原始的10个候选词的概率分布差异性较大,明显倾向于选择第7个词。而使用温度采样重缩放之后,10个候选词的概率分布均匀了很多,选词的多样性得到了明显提升。而概率分布的差异程度可以通过超参数T进行控制:T越大,概率分布越接近均匀分布,也就是模型越倾向于选择偏门的词汇;反之,T越小,概率分布越不均匀,模型越倾向于选择出现概率大的词汇。一般来说,温度对生成效果有如下影响:温度小可能会导致生成重复的内容,而温度大时可能导致生成不连贯或不合逻辑的内容。
读到这里,就可以理解OpenAI
API中temperature和top_p参数的意义了:
temperature: What sampling temperature to use, between 0 and 2. Higher values like 0.8 will make the output more random, while lower values like 0.2 will make it more focused and deterministic. We generally recommend altering this or
top_pbut not both.top_p: An alternative to sampling with temperature, called nucleus sampling, where the model considers the results of the tokens with top_p probability mass. So 0.1 means only the tokens comprising the top 10% probability mass are considered.
总结
本质上,几种不同的解码策略都是优化解码词概率分布,通过缩放,增加可选词的多样性,同时不损失通顺度。但它们都引入了一个新的超参数,在实际应用中,还需要进一步的启发式调优。
此外,解码策略的选择不是非黑即白的问题,需要在不同场景下具体分析和选择。贪心搜索和集束搜索虽然简单,但并不意味着它们的效果总是较差。有研究证明,训练合适的情况下,它们能生成比核采样更好的文本序列。