大模型的涌现能力是幻象?
“涌现能力”可谓是大模型的神来之笔:这些能力在小规模模型中不存在,而仅在大规模模型中存在。涌现能力的神奇之处就在于两点:第一,锐利性,似乎它们瞬间从不存在变为存在;第二,不可预测性,不知道在什么规模的模型上就突现了。
涌现能力相关的讨论在大模型出圈之后一直被津津乐道,尤其是在训练出的模型能力不达预期时,时常背锅:可能是模型不够大,所以不具备这样的能力。问题来了,涌现能力是否真的是大规模模型才拥有的魔法?
NeurIPS 2023的Main Track Outstanding Paper的二者之一,提出了对涌现能力的一种解释:对于特定任务和模型,在分析模型输出时,涌现能力的出现是由于研究人员选择的衡量指标所致,而非模型行为随着规模扩大而发生了根本性变化。具体而言,非线性或不连续的衡量标准会产生明显的涌现能力,而线性或连续的度量标准会导致模型性能的平滑、连续、可预测的变化。
# Announcing the NeurIPS 2023 Paper Awards
# Are Emergent Abilities of Large Language Models a Mirage?
简介
复杂系统的涌现性质长期以来一直被各种学科中进行研究,包括物理学、生物学和数学等领域。物理学家P.W.安德森(P.W. Anderson)的《More Is Different》推崇了涌现性的概念,该书认为随着系统复杂度的增加,可能会出现新的性质,即使基于对系统微观细节的定量理解也无法预测。最近,在观察到大语言模型如GPT、PaLM和LaMDA展现出所谓的“涌现能力”之后,涌现性的概念在机器学习领域引起了极大关注。
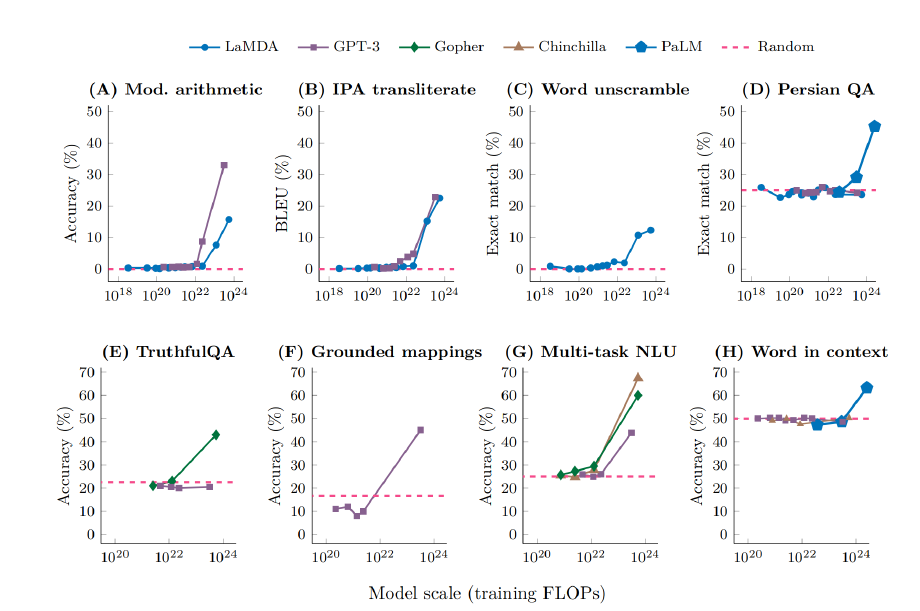
“LLM的涌现能力”被定义为“在较小规模模型中不存在但在大规模模型中存在的能力。因此,无法通过简单地推断在较小规模模型上的性能改进来预测它们”。这样的能力最初是在GPT-3系列模型中发现的。随后的研究强调了这一发现,指出“尽管模型在一般层面上的性能是可预测的,但在特定任务上,性能有时会在尺度上以令人难以预测和突然的方式出现”。这些工作共同确定了LLM中涌现能力的两个定义性质:
- 锐利性:在瞬间从不存在过渡到存在
- 不可预测性: 在看似无法预测的模型规模下发生转变
于是就引发了一系列问题:
- 是什么决定了涌现哪些能力?
- 是什么决定了何时涌现?
- 如何让期待的能力更快出现,并确保不良的能力永远不会出现?
这些问题对于人工智能的安全性和对齐性尤为重要,因为新出现的能力预示着更大的模型可能在某一天突然掌握危险能力。
涌现现象的解释
平滑、连续、可预测的模型性能是呈现出突现和不可预测的特点的呢?答案是选择非线性或不连续的度量标准的原因。
首先,我们认为同一个模型系列,随着规模的增加,对应的test loss也是连续降低的。而这个基本假设基于模型的scaling law:test loss是一个关于训练集大小,参数规模及计算量的函数。
如果一个模型有\(N\)个参数,那么它token级的交叉熵损失可以表示为:
\[\mathcal{L}_{CE}(N)=(\frac{N}{c})^\alpha\]
那么模型选择一个正确token的概率可表示为:
\[p(\text{single token correct})=\exp(-\mathcal{L}_{CE}(N))=\exp(-(\frac{N}{c})^\alpha)\]
举个例子,如果一个指标需要模型正确选择\(L\)个token,如果全部选对则记为1,否则记为0,那么此指标的准确率为:
\[Accuracy(N) \approx p(\text{single token correct})^{L} ={\exp(-(\frac{N}{c})^\alpha)}^L\]
显然,该准确率指标随着\(L\)的增加而呈现非线性性质。因此,如果按该指标画出性能曲线,就会呈现锐利的、不可预测的曲线。与之对应,如果选择一个线性指标,如token的编辑距离可被近似计算为:
\[Accuracy(N) \approx L* (1 - p(\text{single token correct})) =L*(1 - {\exp(-(\frac{N}{c})^\alpha)})\]
采用这样的线性指标进行评估,模型性能就会变得平滑、连续并可预测了。
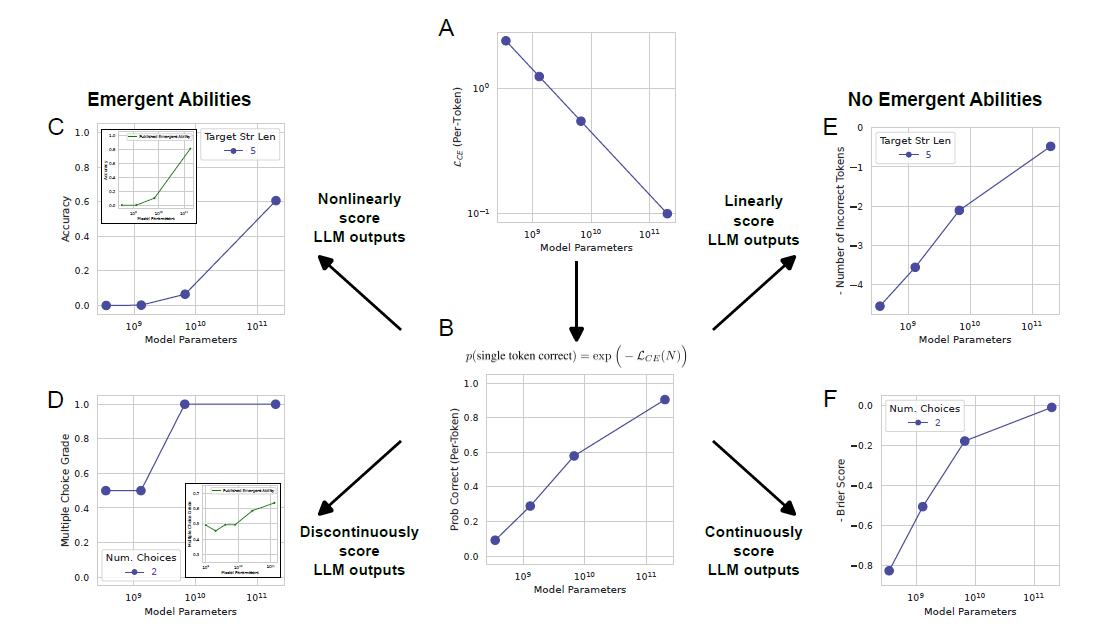
总结一下,涌现能力的产生可被三个因素完全解释:
- 选择了一个非线性或不连续缩放单token错误率的指标
- 估算较小参数规模模型性能时分辨率不足
- 估算较大参数规模模型的采样不足
实验
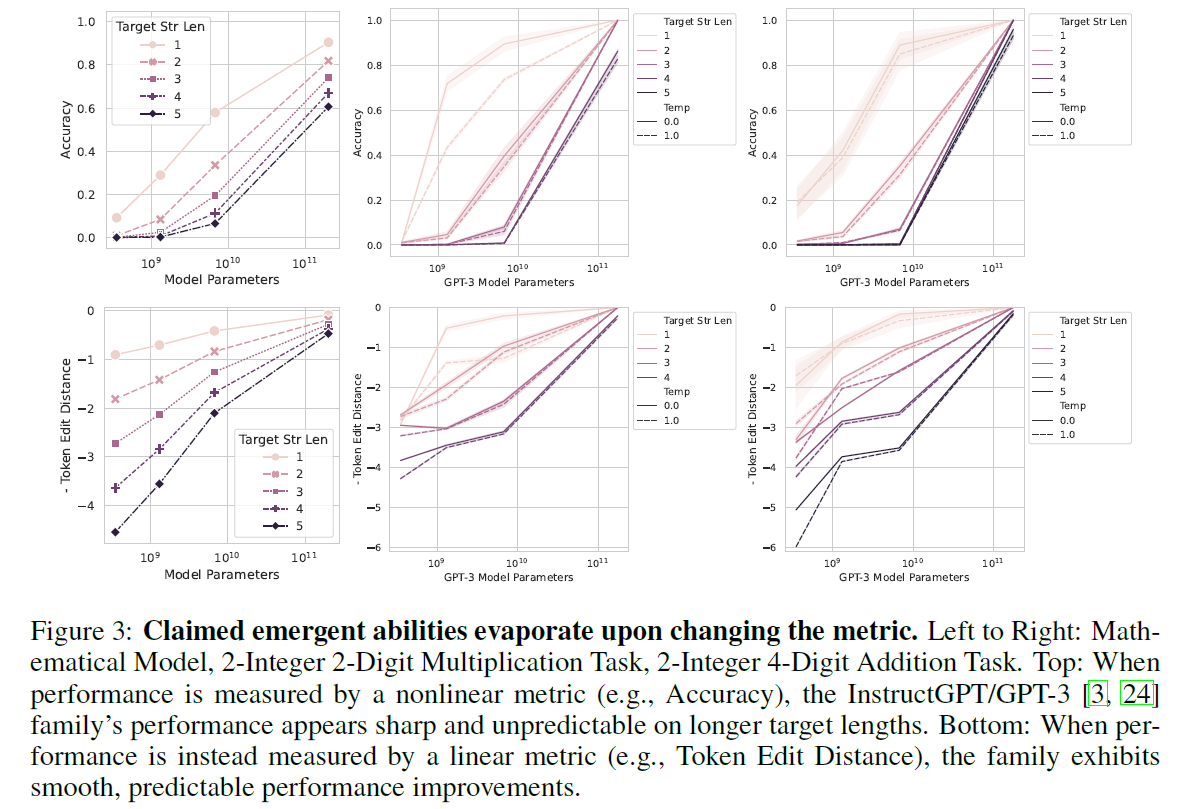
GPT-3的数学涌现能力消失
改变指标,则涌现能力消失。
从左到右:2整数2位数乘法任务,2整数4位数加法任务。
上面:使用非线性指标(例如准确度)衡量模型性能时,InstructGPT/GPT-3系列在较长的目标长度上呈现出锐利且不可预测的性能。 下面:使用线性指标(例如标记编辑距离)衡量模型性能时,该系列展示出平稳、可预测的性能改进。
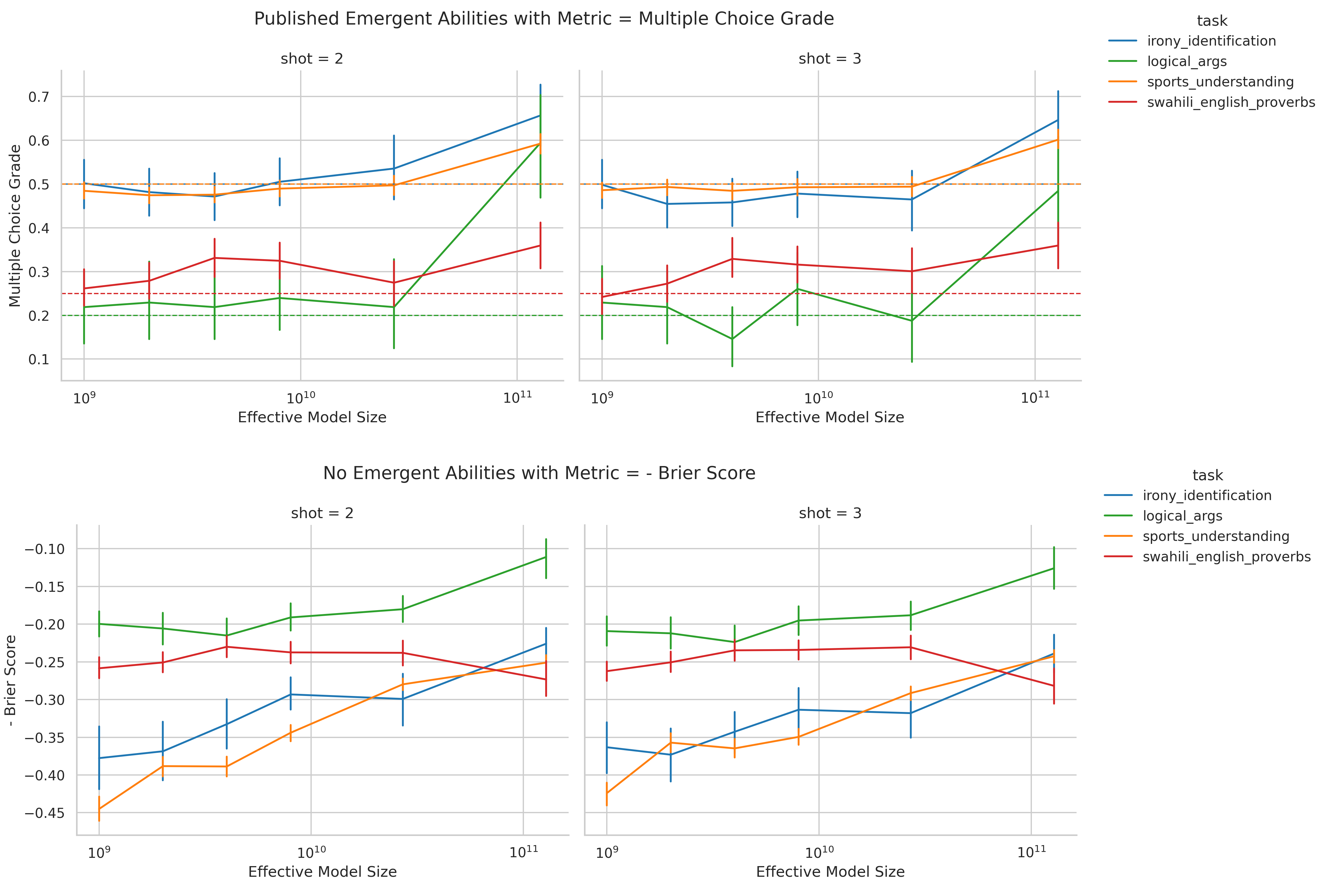
LaMDA的涌现能力消失
涌现能力仅与指标相关,而与任务-模型无关。
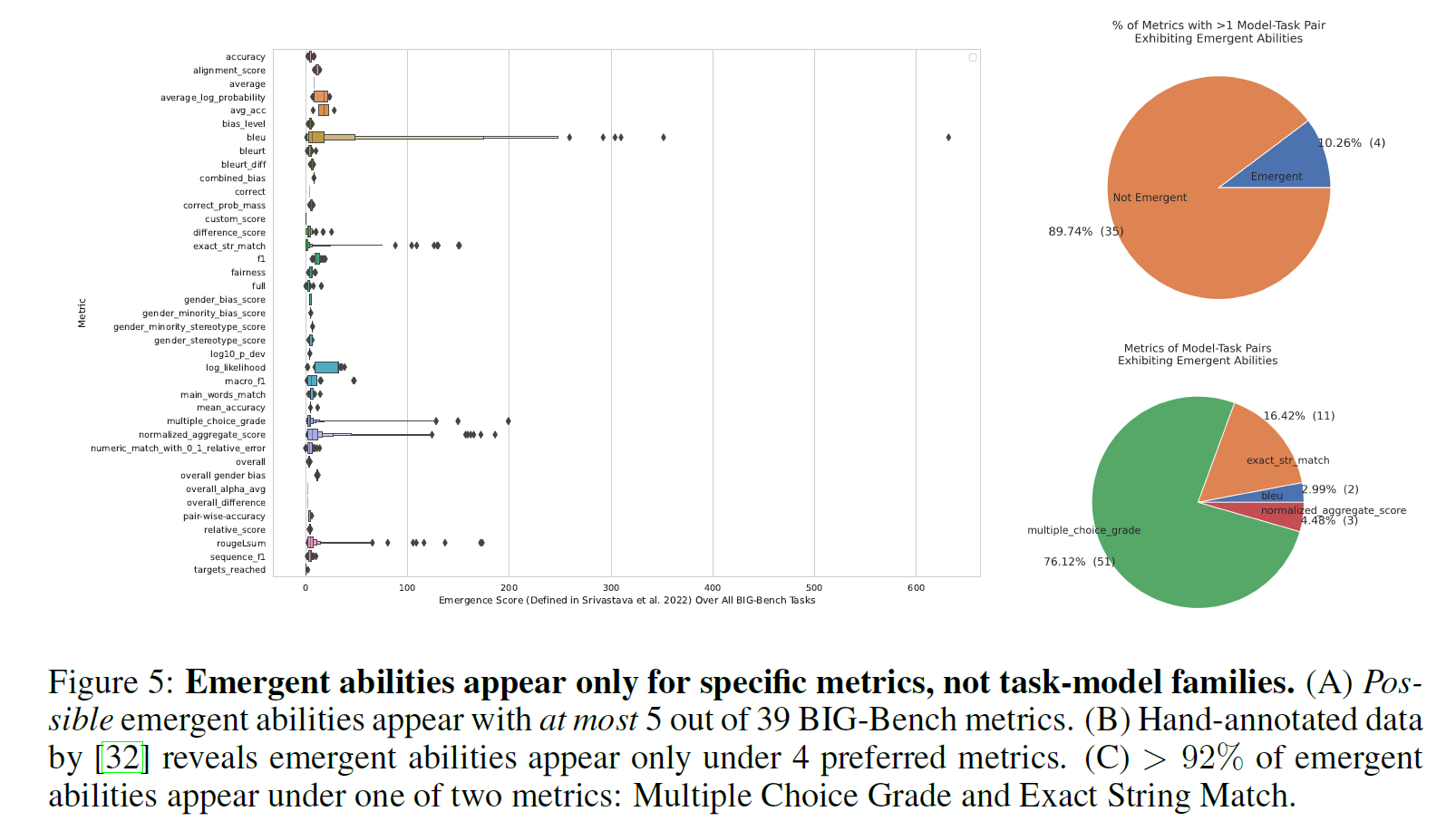
从BIG-Bench的涌现能力评估来看:
- 在39个指标中,仅有5个出现了涌现能力
- 手工标注的结果显示,涌现能力仅在4个指标下出现
- 超过92%的涌现能力都在两个非线性指标之一中出现:多项选择(Multiple Choice Grade)和精确字符串匹配(Exact String Match)。
当使用Brier Score而非Multiple Choice Grade评估LaMDA之后,涌现能力消失:
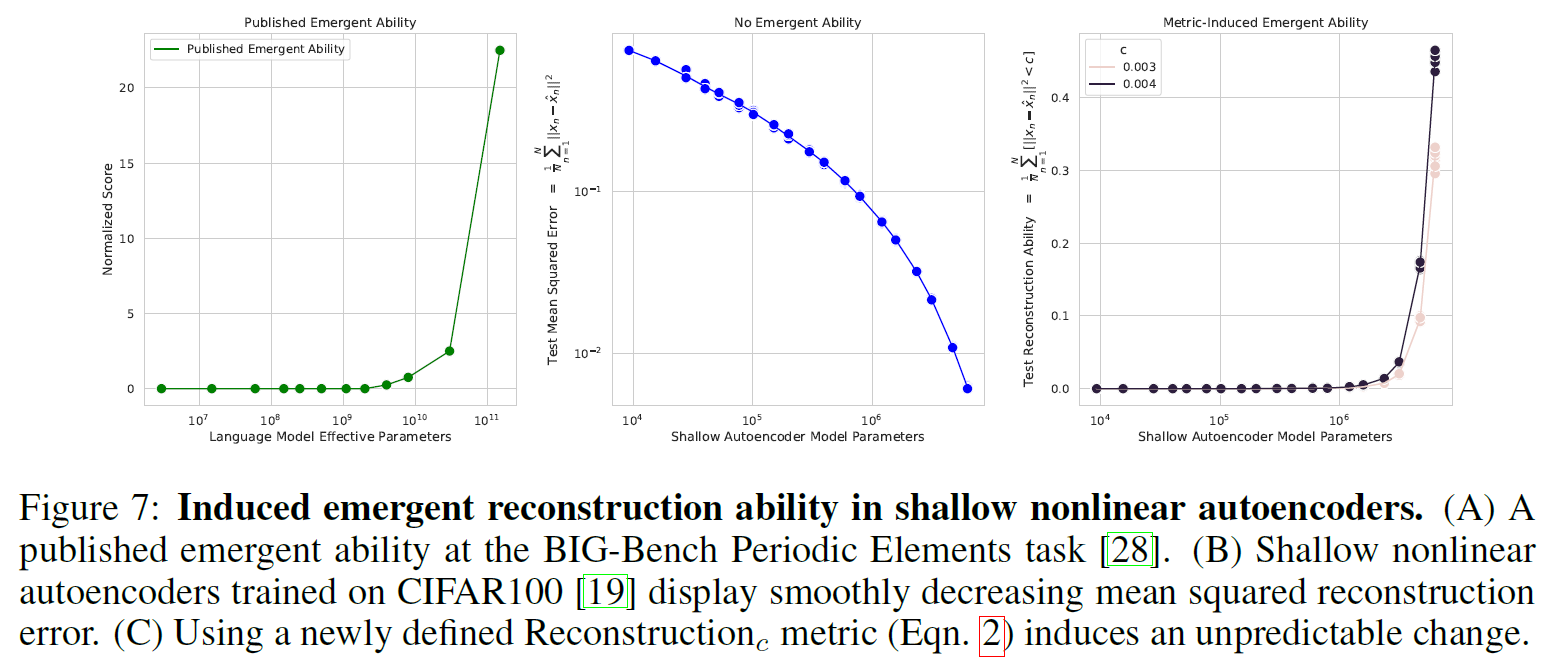
在视觉任务中诱导涌现能力
论文还演示了如何在各种架构的深度网络中诱导涌现能力,包括全连接、卷积和自注意力网络。这里专注于视觉任务的原因在于,视觉模型的能力并没有观察到涌现性。这也是为什么大语言模型的涌现能力被认为如此有趣的原因。
在CIFAR100数据集上重建图像任务的结果如下,从左至右:发表的涌现能力结果;线性指标显示无涌现能力;新定义了非线性指标“产生”了涌现能力:
一个图像分类任务的结果如下,从左至右:在MMLU上发表的涌现能力结果;线性指标显示无涌现能力;新定义了非线性指标“产生”了涌现能力:
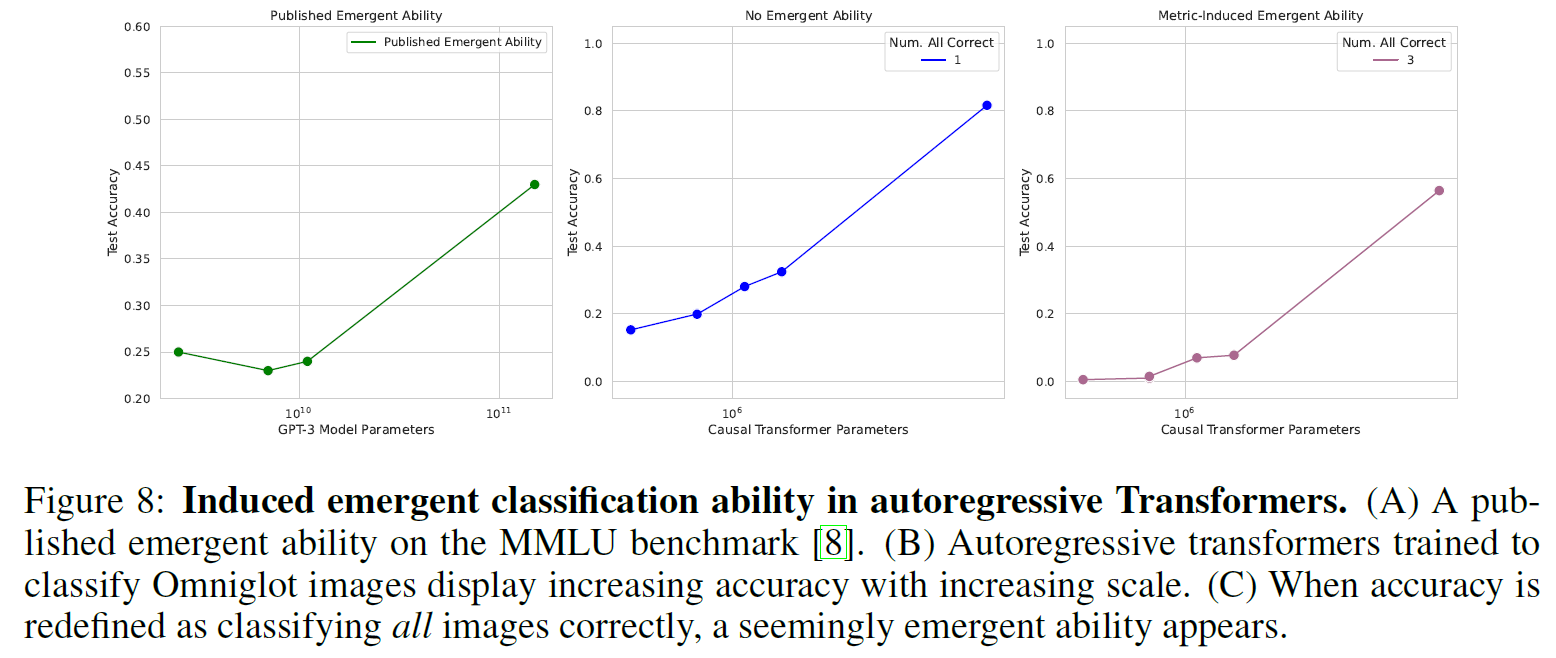
通过这些实验,表明涌现能力在不同的指标或更好的统计方法下会消失,可能涌现能力并非是大规模模型才拥有的基本属性。
总结
指标选择很可能是涌现能力出现的主要原因。涌现能力最常出现在不连续的多项选择任务上。涌现能力可以通过定义不连续的指标诱导产生。
同时,论文也并未否认大模型不能产生涌现能力,而主要想说明之前声称的涌现能力很可能是由于指标选择不当所引发的一种幻象。
不过,从此再遇到模型效果不达预期之时,就不好甩锅是因为模型规模不够大,所以没出现涌现能力了 :-)。
这篇论文在去年4月底就发布了,研究的问题很有趣也很有意义,解释和实验也很扎实,最佳论文奖实至名归。